Poisson disk sampling for arbitrary surfaces

Duan Gao

Algorithm (Euclidean distance)

This algorithm was proposed in [1]. The goal is to sample a set of points with poisson disk distribution on surfaces.

Alogirhtm pipeline:

1. Compute a dense initial random point sets $S_i$ on the surface ($|S_i| = N$)

   1. build 1D distribution based on the surface area of shapes;
   2. sampling $N$ points from the distribution.

   In Mitsuba [2], the default $N$ is $\frac{15A}{\pi r^2}$. Mitsuba has implemented this algorithm too (bluenoise.cpp).

2. Parition $S_i$ into cells

   • compute cell size $r/\sqrt{3}$ and grid resolution
   • For each point in $S_i$, compute the cell it belongs to and assign the cell id to each point.

   For each cell, we need to maintain a list of all points inside it.

   We don't need to allocate such list actually, just sort $S_i$ with cell_id as the key.

   Due to the surface that we sampled is always sparse in 3D, it's better to use a hash table to represent the grid instead of 3D arrays. (invalid cells (no point inside it) will never be considered.)

   We can use std::unordered_map<size_t, Cell> to store all the valid cells.

3. Create phase group

   There will be conflicts if we just perform sampling in each cell parallelly. (nearby cell (mininum distance smaller than $r$) may have conflicts).

   Phase group is a set of cells and there are no conflicts when processed in parallel.

   

   For example, in this figure (from original paper), all cells with the same color with 1 are in one phase group: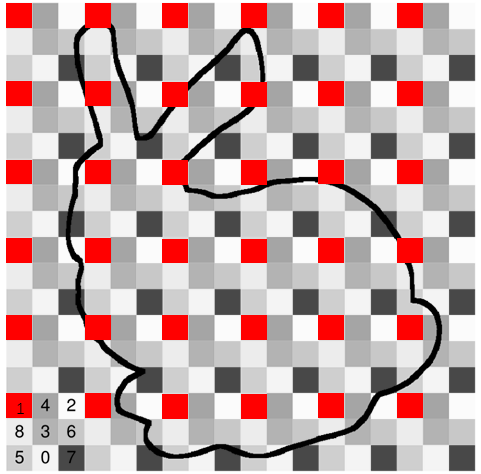

   

   And all cell with the same color with 2 are in one phase group too, etc.

   

   The cells in one phase group are far enough so there in no conflicts between them.

4. Sample blue noise points

   For each phase group:

   for each cell in this phase group:

   for t in range(K): // maximum number of trials per grid cell

   cell[t] is current candidate point.

   if there is some point already be sampled in this cell, ignore it.

   check is there any conflict with the sampled point in neighboring cells.

   if yes, ignore;

   else, accept this candidate.

Sampling with Geodesic distance

• Geodesic distance approximation

  Use the position and normal to estimate the geodesic distance between two points on the surface.

  $$v = (p_2 - p_1) / d_e \\ c_1 = n_1 \cdot v \\ c_2 = n_2 \cdot v \\ d_g(p_1, p_2) = \left\{ \begin{aligned} &\frac{\arcsin{c_1} - \arcsin{c_2}}{c_1-c_2}, & & c_1\neq c_2 \\ &\frac{d_e}{\sqrt{1-c_1^2}}, & & c_1 = c_2 \\ \end{aligned} \right. \\$$

• Other details

  If geodesic distance is used, there might be more than one sampled point inside a cell. So we need consider all of these candidates.

  In implementation, we need mirror changes to code:

  • Use geodesic distance instead of euclidean distance.
  • In Cell data struture, store a list of sampled points' indices instead of single index.
  • In bluse noise sampling, we cannot stop test even there already are some sampled points.
  • In the neighboring conflict testing, we need check all sampled points in the neighboring cells.

Results

I implement this algorithm in my renderer Elegans.

Here are some examples:

Note: $\rho$ is a quality criteria of poisson disk sampling.(Eq-6 in [1])

• Blue noise sampling vs. White noise sampling (randomly sample the same number of points)

  euclidean distance are used in this example.

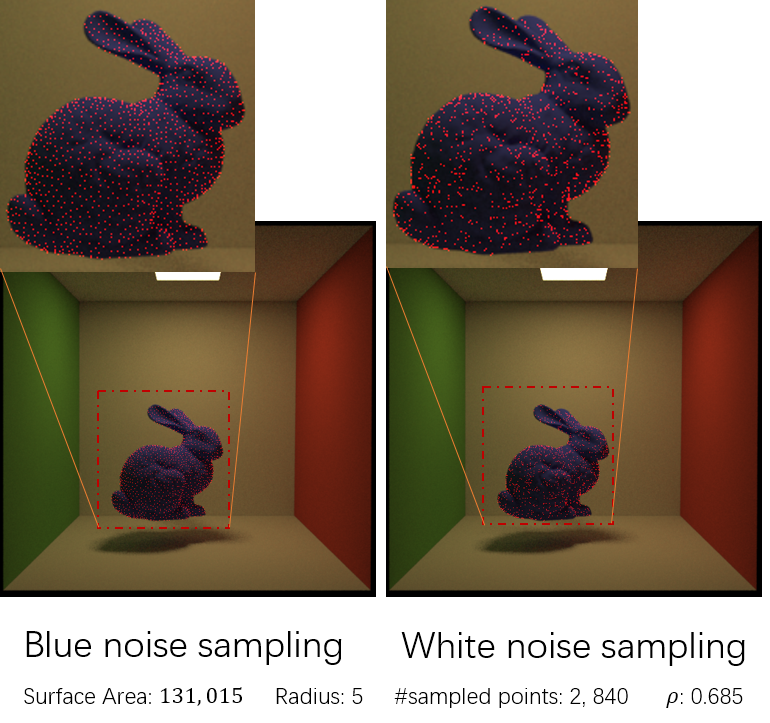
Notes about the visualization:

• Generate blue noise points;
• Project each 3D point to 2D screen space(world -> camera -> raster);
• Emit shadow ray (camera => current point) in camera space to test the visibility and draw a dot only if it passes the test.

For more details, please see the source code of ELEGANS::test_blue_noise_sampling() in test_blue_noise_sampling.cpp.

• Comparison between euclidean distance and geodesic distance

  For a very thin box, if we use euclidean distance in sampling, two points in different faces will cause conflicts; if we use geodesic distance, these two points are far away in fact.

  Note: it's not easy to visualize the difference. I list the number of sampled points which indicates some conflicts are eliminated with geodesic distance.

  We can see the comparison in the following table:

  	Euclidean distance	Geodesic distance
  #init points	20000	20000
  radius	5	5
  #sampled points	1383	1436

   

[1] Bowers J, Wang R, Wei L Y, et al. Parallel Poisson disk sampling with spectrum analysis on surfaces[C]//ACM Transactions on Graphics (TOG). ACM, 2010, 29(6): 166. http://graphics.cs.umass.edu/pubs/sa_2010.pdf [2] Wenzel J. Mitsuba renderer. http://www.mitsuba-renderer.org. 2010.